Today, in this article I’m going to tell you about some important types of questions that are related to linear equations in two variables class 10th.
If you are a 10th class student and looking for linear equations in two variables class 10th, it’s the right place for you.
Linear equation questions are very important whether they’re related to one variable or two variables.
However, I’m going to tell here linear equations in two variables class 10th.
Hence, without wasting your valuable time, let’s start the topic that is about linear equations in two variables class 10th.
Are you interested to solve advanced simplification questions ?
Linear Equations in Two Variables Class 10th –
Here are some important types of linear equation questions for which you can practice more.
1. If a-b=10 and a+3b=110, find the value of a and b.
( a ) 15 & 25
( b ) 30 & 20
( c ) 10 & 20
( d ) 35 & 25
Solution –
a-b=10 and a+3b=110 ( given )
a-b=10………(1)
a+3b=110………(2)
Multiplying by 3 in equation 1
3a-3b=30………(3)
Now, adding the equations 2 and 3
a+3b+3a-3b=110+30
4a=140
a=35 ( Ans )
Putting the value of a in the equation 2 or 3
3×35-3b=30
105-3b=30
105-30=3b
3b=75
b=25 ( Ans )
2. Solve these equations \frac{x-1}{y-1}=\frac{1}{3} and \frac{x+1}{y+1}=\frac{1}{2}
( a ) x=5 & y=8
( b ) x=9 & y=7
( c ) x=3 & y=7
( d ) x=4 & y=8
Solution –
\frac{x-1}{y-1}=\frac{1}{3}
3x-3=y-1
3x-y=2…….(1)
\frac{x+1}{y+1}=\frac{1}{2}
2x+2=y+1
2x-y=-1…….(2)
Subtracting the equations
3x-y-2x+y=2-(-1)
x=3 ( Ans )
Putting the value of x in the equation 1 or 2
3×3-y=2
9-y=2
y=7 ( Ans )
3. A boat covers 24 km upstream and 36 km downstream in 6 hours, while it covers 36 km upstream and 24 km downstream in 6\tfrac{1}{2} hours. Find the speed of the current.
( a ) 5 km/h
( b ) 2 km/h
( c ) 3 km/h
( d ) 7 km/h
Solution –
Let the speed of the boat in still water x km/h and the speed of the current y km/h
\frac{24}{x-y}+\frac{36}{x+y}=6h
\frac{36}{x-y}+\frac{24}{x+y}=\frac{13}{2}h
Let a=\frac{1}{x-y} and b=\frac{1}{x+y}
then, 24a+36b=6……..(1)
36a+24b=13/2……..(2)
Multiplying by 2 in equation 1 and multiplying by 3 in equation 2
(24a+36b=6)×2= 48a+72b=12……..(3)
(36a+24b=13/2)×3=108a+72b=39/2……..(4)
Now, subtracting 3 & 4
48a+72b-108a-72b=12-39/2
-60a=-15/2
a=1/8
Putting the value of a in the equation 3 or 4
48×1/8+72b=12
6+72b=12
72b=6
b=1/12
It means,
a=\frac{1}{x-y}=1/8
x-y=8……..(5)
and
b=\frac{1}{x+y}=1/12
x+y=12……..(6)
Subtracting 5 & 6
x-y-x-y=8-12
-2y=-4
y=2 Km/h ( speed of the current )
4. A, B and C are three sisters. Four years ago, A was twelve less than twice the sum of the ages of B and C. After eight years, A will be two less than the sum of the ages of B and C. Find the Present age of A.
( a ) 15 years
( b ) 11 years
( c ) 12 years
( d ) 36 years
Solution –
Let the present ages of A, B and C are x, y and z.
According to the first condition
x-4=2(y-4+z-4)-12
x-4=2(y+z-8)-12
Let y+z = a
Then, x-4=2(a-8)-12
x-4=2a-16-12
x-4=2a-28
x-2a=-24…….(1)
According to the second condition
x+8=(y+8+z+8)-2
x+8=(y+z+16)-2
x+8=(a+16)-2
x+8=a+14
x-a=6…….(2)
Multiplying by 2 in the equation 2
(x-a=6)×2
2x-2a=12…….(3)
Subtracting 1 & 3
x-2a-2x+2a=-24-12
-x=-36
x=36 years ( the present age of A )
5. If the sum of two numbers is 3 and the sum of their squares is 12, find the product of their numbers.
( a ) -3/2
( b ) 5/2
( c ) 5
( d ) 7/2
Solution –
Let the numbers are x and y.
According to the question
x+y=3…….(1)
x²+y²=12……(2)
Squaring both the sides of equation 1
(x+y)²=(3)²
x²+y²+2xy=9
Put x²+y²=12 ( given )
12+2xy=9
2xy=9-12
2xy=-3
xy=-3/2 ( Ans )
6. Eight years ago, Atul’s age was ten times of his son and after two years Atul’s age will be four times of his son. Find the present ages of both.
( a ) 35 years and 20 years
( b ) 25 years and 10 years
( c ) 48 years and 12 years
( d ) 16 years and 4 years
Solution –
Let the present ages of Atul and his son are a and b.
According to the first condition
a-8=10(b-8)
a-8=10b-80
a-10b=-72
a-10b=-72……(1)
According to the second condition
a+2=4(b+2)
a+8=4b+8
a-4b=0
a=4b…….(2)
Putting the value of a in the equation 1
4b-10b=-72
-6b=-72
b=12 years ( the age of Atul’s son )
Putting the value of b in the equation 1 or 2
a=4×12
a=48 years ( the age of Atul )
7. The Policeman and the thief are 150 meters apart from each other. When the policeman starts the chase, the thief also starts running. If they go in the same direction, they meet in 15 sec and if they go in the opposite direction they meet in 10 sec. Find their speeds.
( a ) 10 m/s and 21 m/s
( b ) 15 m/s and 25 m/s
( c ) 2.5 m/s and 12.5 m/s
( d ) 2 m/s and 12 m/s
Solution –
When they go in the same direction, let the distance travelled by the thief in 15 sec is x by V1 speed and the distance travelled by the policeman in 15 sec is y by V2 speed.
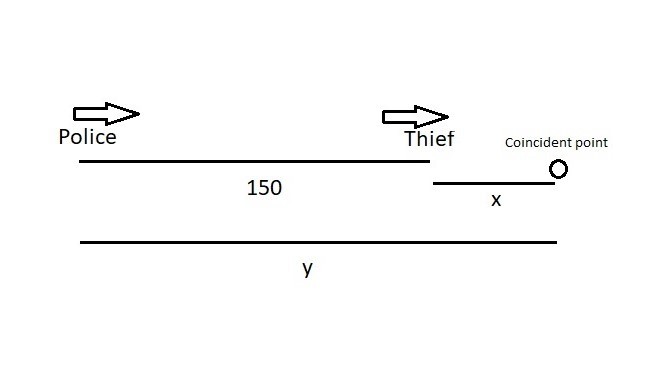
y=150+x
V2×15=150+V1×15
15V2=150+15V1
15V2-15V1=150
divided by 15
V2-V1=10…….(1)
When they go in the opposite direction, let the thief covers a distance of x meters and the policeman covers the distance of y meters.
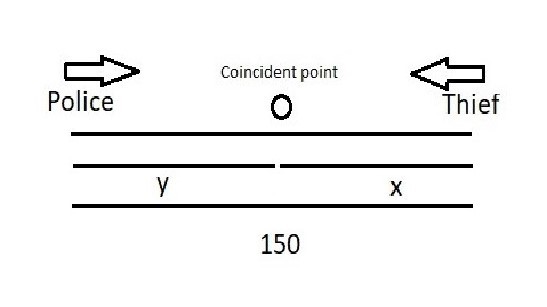
It means, x+y=150
V1×10+V2×10=150
10V1+10V2=150
Divided by 10
V1+V2=15…….(2)
Adding equations 1 and 2
V2-V1+V1+V2=10+15
2V2=25
V2=12.5 m/s ( speed of the policeman )
Putting the value of V2 in equation 1 or 2
12.5-V1=10
V1=2.5 m/s ( speed of the thief )
8. If ax+by-a+b=0 and bx-ay-a-b=0, then find the value of x and y.
( a ) x=3 & y=8
( b ) x=5 & y=-5
( c ) x=2 & y=4
( d ) x=1 & y=-1
Solution –
ax+by-a+b=0 ( given )
Multiplying by a
(ax+by-a+b=0)×a
a²x+aby-a²+ab=0…….(1)
bx-ay-a-b=0 (given )
Multiplying by b
(bx-ay-a-b=0)×b
b²x-aby-ab-b²=0…….(2)
Adding both the equations
a²x+aby-a²+ab+b²x-aby-ab-b²=0
a²x-a²+b²x-b²=0
a²x+b²x-a²-b²=0
a²x+b²x=a²+b²
x(a²+b²)=a²+b²
x=1 ( Ans )
Putting the value of x in the equation 1 or 2
a²×1+aby-a²+ab=0
a²+aby-a²+ab=0
aby+ab=0
aby=-ab
y=-1 ( Ans )
9. In the given figure, ABCD is a rectangle. Find the value of L²+M².
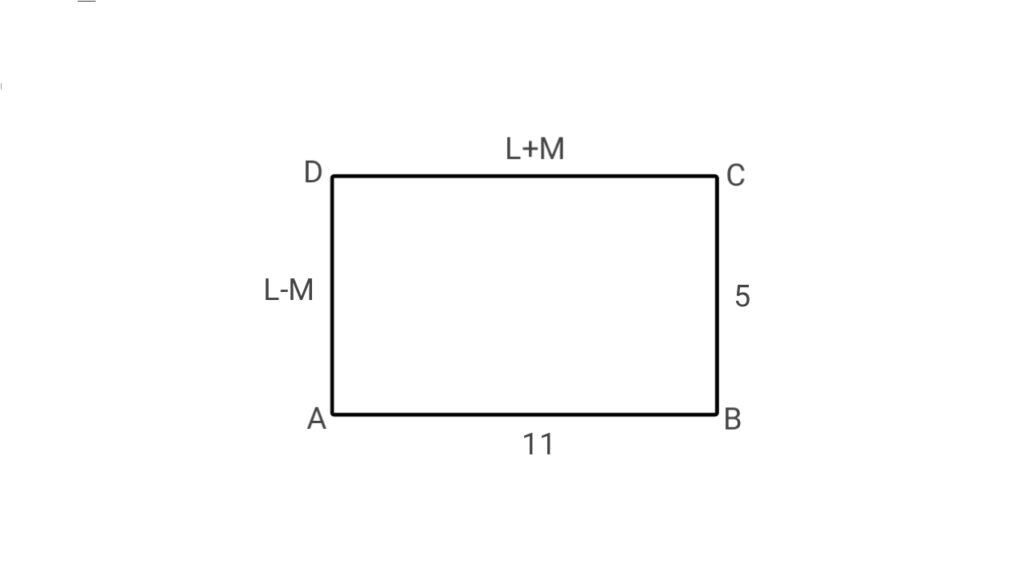
( a ) 70
( b ) 73
( c ) 72
( d ) 74
Solution –
L-M=5…….(1)
L+M=11…….(2)
Adding both the equations
L-M+L+M=5+11
2L=16
L=16/2
L=8
Putting the value of L in the equation 1 or 2
8-M=5
M=3
Now, L²+M²=(8)²+(3)²=64+9=73
L²+M²=73 ( Ans )
10. If the angles of a cyclic quadrilateral ABCD are ∠A=(4x+5)°, ∠B=(10)°, ∠C=(2x+y)°, ∠D=(5y-5)°, find the value of x and y.
( a ) 23.3° and 35°
( b ) 68° and 55°
( c ) 40° and 68.5°
( d ) 50° and 45°
Solution –
As we know, the sum of the opposite angles in a cyclic quadrilateral is 180° so ∠A+∠C=180° and ∠B+∠D=180°
Now,
∠A+∠C=180°
4x+5+2x+y=180
4x+2x+y=180-5
6x+y=175°…….(1)
∠B+∠D=180°
10+5y-5=180
5y+5=180
5y=180-5
5y=175
y=35° ( Ans )
Putting the value of y in the equation 1 or 2
6x+35=175°
6x=140°
x=140/6
x=23.3° ( Ans )
11. Solve the equations 2x+\frac{3}{y}=8 and 3x-\frac{4}{y}=7 for the value of x and y.
( a ) 9 and 7
( b ) 18.7 and 1.7
( c ) 5.5 and 2.8°
( d ) 4 and 2
Solution –
2x+\frac{3}{y}=8 ( given )
Multiplying by 3
6x+\frac{9}{y}=24…….(1)
3x-\frac{4}{y}=7 ( given )
Multiplying by 2
6x-\frac{8}{y}=14…….(2)
Subtracting the equations
6x+\frac{9}{y}-6x+\frac{8}{y}=24-14
\frac{9}{y}+\frac{8}{y}=10
17/y=10
y=17/10
y=1.7 ( Ans )
Putting the value of y in the equation 1 or 2
6x+\frac{9}{1.7}=24
6x+\frac{90}{17}=24
6x=24-\frac{90}{17}
6x=\frac{408-90}{17}
x=318/17
x=18.7 ( Ans )
12. The speed of a boat is 24 km/h in still water. It takes 1 hour more to go 32 km upstream than to return downstream to the same place. Find the speed of the stream.
( a ) 5
( b ) 11
( c ) 8
( d ) 7
Solution –
Let the speed of the boat in still water is V1, the speed of the stream is V2, time taken in upstream by the boat is T1 and time taken in downstream by boat is T2.
V1=24 km/h…….(1) ( given )
According to the question
T1=T2+1
\frac{32}{V1-V2}=\frac{32}{V1+V2}+1…….(2)
Putting the value of V1 in the equation 2.
32[\frac{1}{24-V2}–\frac{1}{24+V2}]=1
[\frac{1}{24-V2}–\frac{1}{24+V2}]=1/32
\frac{24+V2-24+V2}{(24-V2)(24+V2)}=1/32
\frac{2V2}{576-V2²}=1/32
64V2=-V2²+576
V2²+64V2-576=0
V2²+(72-8)V2-576=0
V2²+72V2-8V2-576=0
V2(V2+72)-8(V2+72)=0
(V2-8)(V2+72)=0
V2-8=0
V2=8 ( the speed of the stream )
Final words –
I hope that the article has proved to be very useful to students who are looking for linear equations in two variables class 10th.
Here, I have described all the most important types of linear equations in two variables class 10th.
At last, if you really like the article that is about linear equations in two variables class 10th, please share it to those who need it.
Thank you.